Stored Energy In An Inductor

Next: The Circuit Upwards: Inductance Previous: Self Inductance

Energy Stored in an Inductor

Suppose that an inductor of inductance

is connected to a variable DC voltage supply. The supply is adjusted so as to increase the current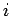

flowing through the inductor from zilch to some final value

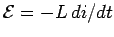. Equally the current through the inductor is ramped upwards, an emf ${\cal E} = - L\,d i/dt$ is generated, which acts to oppose the increase in the current. Clearly, work must exist done against this emf past the voltage source in order to establish the current in the inductor. The work washed by the voltage source during a time interval

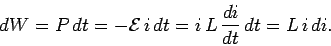$\begin{displaymath} d W = P\,dt = -{\cal E}\,i\,dt = i\,L\,\frac{d i}{d t} \,d t = L\,i\,di. \end{displaymath}$

(247)

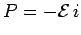Here, $P=-{\cal E}\,i$ is the instantaneous rate at which the voltage source performs work. To find the full work

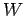done in establishing the final current

in the inductor, we must integrate the above expression. Thus,

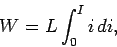$\begin{displaymath} W = L\int_0^I i\,di, \end{displaymath}$

(248)

giving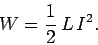

$\begin{displaymath} W = \frac{1}{2}\,L\,I^2. \end{displaymath}$

(249)

This energy is actually stored in the magnetic field generated by the current flowing through the inductor. In a pure inductor, the energy is stored without loss, and is returned to the rest of the excursion when the current through the inductor is ramped down, and its associated magnetic field collapses.

Consider a simple solenoid. Equations (244), (246), and (249) can be combined to give

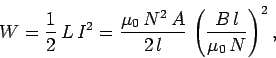$\begin{displaymath} W = \frac{1}{2} \,L\,I^2 =\frac{\mu_0\,N^2\,A}{2\,l} \,\left(\frac{B\,l}{\mu_0\,N} \right)^2, \end{displaymath}$

(250)

which reduces to

$\begin{displaymath} W = \frac{B^2}{2\,\mu_0} \,\,l\,A. \end{displaymath}$

(251)

This represents the energy stored in the magnetic field of the solenoid. However, the volume of the field-filled cadre of the solenoid is 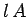$l\,A$ , and then the magnetic energy density (i.e., the energy per unit of measurement book) inside the solenoid is 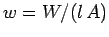$w = W/(l\,A)$ , or

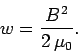$\begin{displaymath} w = \frac{B^2}{2\,\mu_0}. \end{displaymath}$

(252)

It turns out that this effect is quite full general. Thus, we can calculate the energy content of any magnetic field past dividing space into trivial cubes (in each of which the magnetic field is approximately uniform), applying the higher up formula to observe the energy content of each cube, and summing the energies thus obtained to observe the total energy.

When electric and magnetic fields be together in space, Eqs. (122) and (252) can be combined to give an expression for the full energy stored in the combined fields per unit volume:

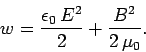$\begin{displaymath} w = \frac{\epsilon_0\,E^2}{2} + \frac{B^2}{2\,\mu_0}. \end{displaymath}$

(253)

Next: The Circuit Up: Inductance Previous: Self Inductance

Richard Fitzpatrick 2007-07-14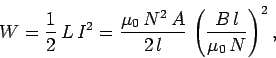

Stored Energy In An Inductor,

Source: https://farside.ph.utexas.edu/teaching/316/lectures/node103.html

Posted by: lumpkinthemeavoking.blogspot.com

Stored Energy In An Inductor

Energy Stored in an Inductor

Stored Energy In An Inductor,

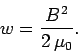
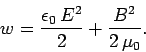
0 Response to "Stored Energy In An Inductor"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel